Adaptive Navigational Recommendations for Urban Transportation

Motivation

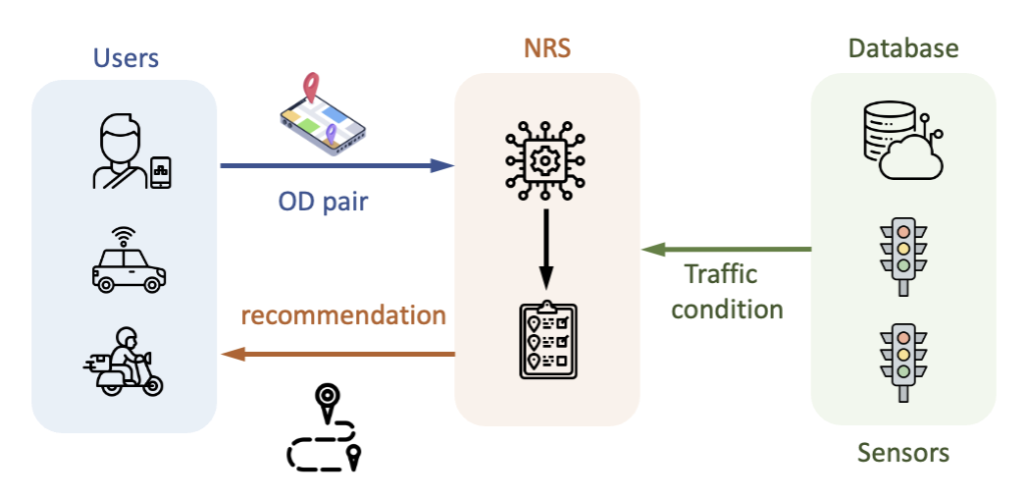
In urban transportation environments, drivers often encounter various path (route) options when navigating to their destinations. This emphasizes the importance of navigational recommendation systems (NRS), which simplify decision-making and reduce travel time for users while alleviating potential congestion for broader societal benefits. However, recommending the shortest path may cause the flash crowd effect, and system-optimal routes may not always align the preferences of human users, leading to non-compliance issues. It is also worth noting that universal NRS adoption is impractical.

Therefore, in this study, we aim to address these challenges by proposing an incentive compatibility recommendation system from a game-theoretic perspective and accounts for non-user drivers with their own path choice behaviors.

Our approach

Interacting directly with human users and being aware of potential non-compliance concerns, NRS must ensure that users lack incentives to unilaterally deviate from the recommendations, which coincides with the concept of Nash equilibrium. Consequently, we suggest that a feasible recommendation provided by the NRS must satisfy the incentive constraints for the users. Furthermore, assuming universal adoption of a specific NRS among all individuals within the urban transportation network is rather impractical. Thus, we also account for non-user drivers who navigate independently based on their own preferences and path choice behaviors.

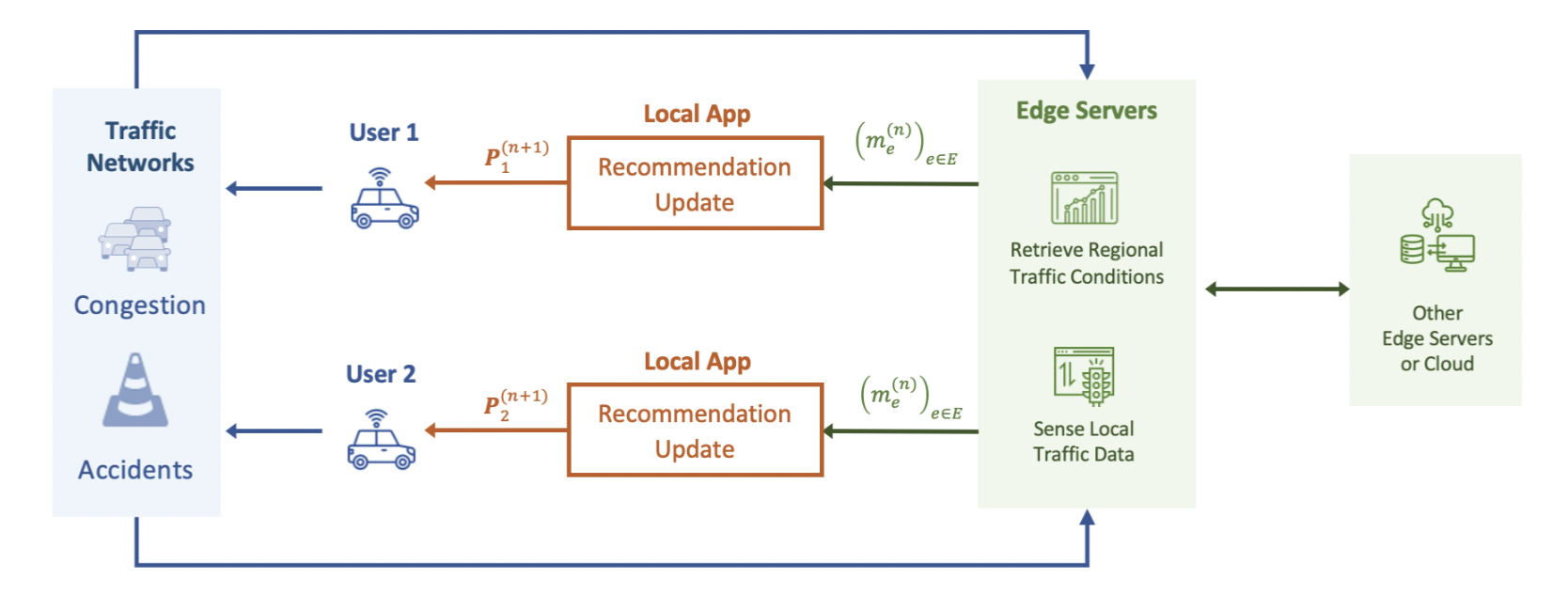
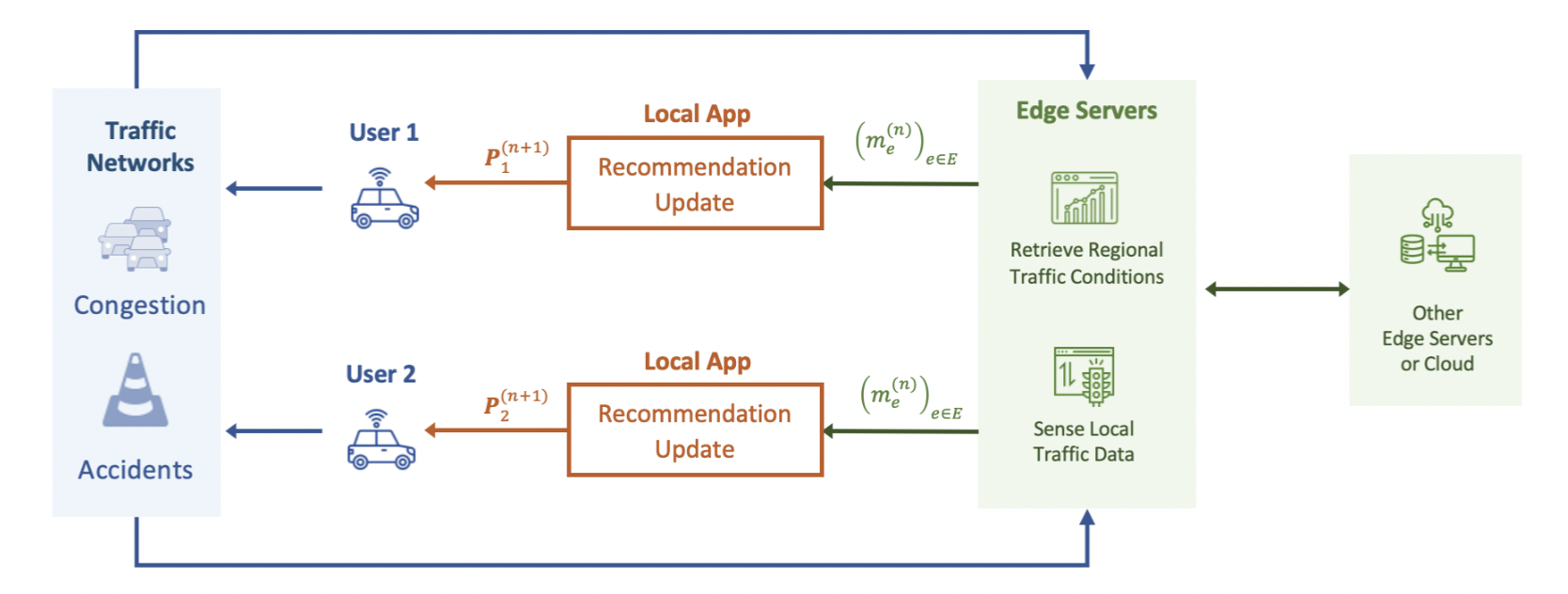
Additionally, recognizing the dynamic nature of traffic conditions and the unpredictability of accidents, we also introduce a dynamic NRS with parallel and random update schemes using projected gradient descent (PGD), aiming to assisting users in safely adapting to changing traffic conditions while ensuring optimal total travel time costs. The following figure shows the update scheme that utilizes vehicle-to-everything (V2X) technologies and the edge computing framework, where the edge server (embedded in the road infrastructure) can collect localized data, exchange regional traffic conditions with other edge servers, and communicate with the local apps associated with NRS users. Then, the local NRS app can compute and provide the updated recommendation for its user.

A bit more on the system model

One of the essential components of NRS is the urban transportation network, represented by $\mathcal{G}=\{\mathcal{V}, \mathcal{E}\}$. In this context, the set of nodes $\mathcal{V}$ corresponds to intersections, while the set of edges $\mathcal{E}$ indicates the roads. Traveling along a road $e\in \mathcal{E}$ will incur a cost $c_e: \mathbb{R}_{\ge 0} \mapsto \mathbb{R}_{+}$ associated with the expected flow $f_e \in \mathbb{R}_{\ge 0}$ on that road $e$. One usual choice for the cost function $c_e(\cdot)$ is the travel time cost

provided by the standard Bureau of Public Roads (BPR) function. Here, $t_e \in \mathbb{R}_{+}$ represents the free-flow travel time on road $e$, $k_e \in \mathbb{R}_{+}$ signifies the capacity of road $e$, and $\eta, \zeta \in \mathbb{R}_{\ge 0}$ are some parameters.

The user set of NRS is denoted as $\mathcal{U}$. Each user, $u \in \mathcal{U}$, is associated with a specific origin $O_u \in \mathcal{V}$ and destination $D_u \in \mathcal{V}$ pair. We refer to the pair as an OD pair, expressed by $\theta_u = (O_u, D_u)$, and the set of OD pairs for the NRS users is $\Theta_{\mathcal{U}} \subset \Theta$, with $\Theta = |\mathcal{V}| \times |\mathcal{V}|$. Then, user $u$ with OD pair $\theta_u$ has the feasible path choice set $\mathcal{S}_u = \{s_{u, 1}, \cdots, s_{u, k_u}\}$. Each choice $s_{u, i} \in \mathcal{S}_u$ provides the user $u$ a path from the origin to the desired destination. %To this end, the factors taken into account by the NRS can be represented as $\mathscr{G}=\left\langle \ \mathcal{G}, (c_e(\cdot))_{e \in \mathcal{E}}, \mathcal{U}, (\mathcal{S}_u)_{u \in \mathcal{U}} \ \right\rangle$.

This study explores the scenario where the NRS recommends a mixed strategy over feasible path choices to the users. Define $\mathcal{P}_u:=\Delta \mathcal{S}_u$ as the simplex of $\mathcal{S}_u$ and $\mathcal{P}:=\Pi_{u \in \mathcal{U}}\mathcal{P}_u$. A mixed strategy for user $u$ is $\textbf{P}_u \in \mathcal{P}_u$ so that $\textbf{P}_u=\{p_{u, i}\}_{i=1, \cdots, k_u}$ is a probability distribution over $\mathcal{S}_u$. Each $p_{u, i}\in[0,1]$ denotes the probability that the NRS recommends path $s_{u, i} \in \mathcal{S}_u$ to user $u$, subject to the constraints $ \sum_{i=1}^{k_u}p_{u, i}=1 , \ \forall u \in \mathcal{U}. $ That is,

which is compact and convex. Then, the recommendations suggested by the NRS to all users is $\textbf{P}=\{\textbf{P}_u\}_{u \in \mathcal{U}} \in \mathcal{P}$.

In transportation, from a microscopic perspective, the probability $p_{u, i}$ can be interpreted as the expected volume generated by user $u$ along path $s_{u, i}$. This, in turn, contributes to the expected flow (load) $f_e^r: \mathcal{P} \mapsto \mathbb{R}_{\ge 0}$ on edge $e \in \mathcal{E}$ as below.

with the indicator function $\mathbf{1}_{\{e \in s_{u, i}\}}$ equal to $1$ if road $e$ is part of path $s_{u, i}$ and $0$ otherwise. Therefore, a generalized travel cost $C_{u, i}: \mathcal{P} \mapsto \mathbb{R}_{+}$ for user $u$ associated with path $s_{u, i}$ can be formulated by summing the costs of all the edges along the path:

We denote the set of drivers who do not use the NRS as $\mathcal{U}_d$. Similar to the users, each driver $d \in \mathcal{U}_d$ is associated with an origin $O_{d} \in \mathcal{V}$ and destination $D_{d} \in \mathcal{V}$ pair, leading to a set of feasible paths $\mathcal{S}_{d} = \{s_{d, 1}, \cdots, s_{d, k_{d}}\}$. Without loss of generality, this work assumes that the stochastic choice behavior of these drivers can be modeled by the Multinomial Logit (MNL) model.

In the context of path choices, the model supposes that individuals make choices based on the value they associate with each available option. That is, the behavior (mixed strategy) of driver $d$ over the set of feasible path choices $\mathcal{S}_{d}$ is given by

where $V_{d, i}=-\alpha_{d}-\beta_{d} C_{{d}, i}^o$ represents the driver’s value of path $s_{d, i}$, with $C_{d, i}^o \in \mathbb R_{+}$ being the current (initial) cost (travel time) on $s_{d, i}$. Here, $\alpha_{d} \in \mathbb{R}$ and $\beta_{d} \in \mathbb{R}$ are driver $d$’s preference parameters. We denote $\textbf{P}_{o}=\{p_{d, i}^o\}_{d \in \mathcal{U}_d, i=1, \cdots, k_{d}}$ as the mixed strategy played by the drivers. Then, the expected flow induced by other drivers on the road $e \in \mathcal{E}$ is $f_e^o: \Pi_{d\in \mathcal{U}_d} \Delta \mathcal{S}_{d} \mapsto \mathbb{R}_{\ge 0}$, where

In situations where the NRS takes into account other drivers, the combined expected flow caused by both users and drivers on each road $e \in \mathcal{E}$ is $f_e: \mathcal{P} \times \Pi_{d\in \mathcal{U}_d} \Delta \mathcal{S}_{d} \mapsto \mathbb{R}_{\ge 0}$, where $f_e(\textbf{P};\textbf{P}_{o}) = f_e^r(\textbf{P}) +f_e^o(\textbf{P}_{o})$, leading to the travel time cost

Thus, the travel cost for user $u$ associated with path $s_{u, i}$ becomes $C'_{u, i}: \mathcal{P} \times \Pi_{d\in \mathcal{U}_d} \Delta \mathcal{S}_{d} \mapsto \mathbb{R}_{+}$, and can be expressed as

where the additional expected flow $f_e^o(\textbf{P}_{o})$ resulting from other drivers’ path choice behaviors $\textbf{P}^o$ does not change with the recommended mixed strategies $\textbf{P}$.

To this end, the elements considered in the context of urban transportation network and taken into account by the NRS can be encapsulated using the notation $\mathscr{R}=\left\langle \ \mathcal{G}, (c_e(\cdot))_{e \in \mathcal{E}}, \mathcal{U}, (\mathcal{S}_u)_{u \in \mathcal{U}}, \mathcal{d}, (\mathcal{S}_{d})_{d \in \mathcal{d}} \ \right\rangle$, and we call $\mathscr{R}$ the ``NRS component’'.

Considering an NRS component denoted as $\mathscr{R}$, a feasible recommendation profile to all the users $\textbf{P} \in \mathcal{P}$ needs to satisfy:

A bit more on the updated scheme

With recent advances in vehicle-to-everything (V2X) technology and edge computing, each user (or the local app associated with each user) is capable of getting the current traffic conditions through edge servers embedded in the road infrastructure. Denote traffic conditions at time step $n$ as $\textbf{m}^{(n)} \in \mathbb{R}_{\ge 0}^{|\mathcal{E}|}$, with $\textbf{m}^{(n)}= (m_e^{(n)})_{e \in \mathcal{E}}$. Recall that each element, represented by $m_e^{(n)}$, comes from the resulting expected flow and define $M_e: \mathcal{P} \times \Pi_{d\in \mathcal{U}_d} \Delta \mathcal{S}_{d} \mapsto \mathbb{R}_{\ge 0}$ so that

After gathering the current traffic conditions $\textbf{m}^{(n)}$, user $u$ can utilize his/her navigational recommendation $\textbf{P}_u^{(n)}$ at time step $n$ to infer the conditions influenced by other users and drivers, denoted as $(\hat{f}_e(\textbf{P}_{-u}^{(n)};\textbf{P}_o^{(n)}))_{e \in \mathcal{E}}$. It is worth noting that the PGD method for solving $\textbf{OP}_u$ requires user $u$ to have access to both the recommendations for other users $\textbf{P}_{-u}$, and the drivers’ behaviors $\textbf{P}_{o}$. However, once the values of $\textbf{m}^{(n)}$ become available to users, local apps (or users) can directly utilize $\textbf{m}^{(n)}$ to update the recommendations. We will discuss two update schemes in the following subsections.

Parallel Update Algorithm

In this section, we explore a parallel update scheme where every user (or local app) synchronously adjusts their recommendation at each time step. By leveraging the traffic condition $\textbf{m}^{(n)}$, we can rewrite the cost function evaluated by user $u$ as $F'_u: \mathcal{P}_u \times \mathbb{R}_{\ge 0}^{|\mathcal{E}|} \mapsto \mathbb{R}_{+}$, where at time step $n$,

Note that $F'_u(\textbf{P}_u^{(n)},\textbf{m}^{(n)})$ and $F_u(\textbf{P}_{u}^{(n)}, \textbf{P}_{-u}^{(n)}; \textbf{P}_o^{(n)})$ have identical value at the same $\textbf{P}_{u}^{(n)}, \textbf{P}_{-u}^{(n)}, \textbf{P}_o^{(n)}$. Then, the gradient of $F'_u$ with respect to each element $p_{u, i}^{(n)}$ of $\textbf{P}_u^{(n)}$ becomes $\partial F'_u/\partial p_{u, i}^{(n)}=$

Let $\nabla_u F'_u =(\partial F'_u/\partial p_{u, i}^{(n)})_{s_{u, i} \in \mathcal{S}_u}$ and denote gradient of $F'_u$ at $\textbf{P}_u^{(n)}, \textbf{m}^{(n)}$ as $\nabla_u F'_u(\textbf{P}_u^{(n)}, \textbf{m}^{(n)})$, starting with some initial point for all users, $\textbf{P}^{(0)} \in \mathcal{P}$, the updated recommendation at time step $n+1$ is, therefore, $\forall u \in \mathcal{U}$,

By denoting $\nabla F'(\textbf{P}^{(n)},\textbf{m}^{(n)})=(\nabla_u F'_u(\textbf{P}_u^{(n)}, \textbf{m}^{(n)}))_{u \in \mathcal{U}}$, we can get:

Under the conditions that for all $u \in \mathcal{U}$, the expected cost $F_u$ is continuously differentiable in $\textbf{P} \in \mathcal{P}$ and convex in $\textbf{P}_u \in \mathcal{P}_u$, the sequence of recommendations $\{\textbf{P}^{(n)}\}$, generated by the equation above, converges to an NE, $\textbf{P}^{*}$. Therefore, the $u$-th component of $\textbf{P}^{(n+1)}$ can be performed locally by the NRS app linked to user $u$. Such distributed gradient updates still lead to the convergence to an NE under mild assumptions.

Main Results

• Our numerical analyses demonstrate that the updated scheme achieves the lowest total user travel time costs while ensuring user engagement and adherence to recommendations.

Some related research (on NRS)

Selfish (individualized) recommendations

One aspect of recommendation systems often focuses on individually optimizing recommendations for each user by suggesting the shortest paths according to current traffic conditions.

However, such individualized (selfish) recommendations tend to overlook the collective impact on other users, potentially leading to the flash crowd effect. That is, if a substantial number of users simultaneously navigate to the same shortest path, it can result in a surge of traffic volume along that path, increasing the overall congestion levels across the urban transportation network.

Papers

• D. E. Knuth, “A generalization of dijkstra’s algorithm,” Information Processing Letters, vol. 6, no. 1, pp. 1–5, 1977.
• H. D. Sherali, K. Ozbay, and S. Subramanian, “The time-dependent shortest pair of disjoint paths problem: Complexity, models, and algorithms,” Networks: An International Journal, vol. 31, no. 4, pp. 259–272, 1998.
• A. Grzybek, G. Danoy, P. Bouvry, and M. Seredynski, “Mitigating flash crowd effect using connected vehicle technology,” Vehicular Communications, vol. 2, no. 4, pp. 238–250, 2015.

System optimal recommendations

Alternatively, recommendation systems may prioritize overall system efficiency by minimizing the total travel time cost over the network. However, this approach can result in disparities where some users experience longer travel times compared to others traveling from the same origin to the same destination. This discrepancy raises concerns regarding user compliance and fairness. The challenge then lies in promoting socially responsible behavior among users, motivating them to accept recommendations that may entail higher travel costs in exchange for alleviating congestion for the collective benefit.

User equilibrium recommendations

On the contrary, recommendation systems can adopt the concept of user equilibrium, as seen in mixed-strategy or pure-strategy atomic routing games. In such equilibrium scenarios, fairness among users is guaranteed, as individuals with the same origin and destination experience identical (minimum) travel times once equilibrium is reached. Following such a case, the user will not have incentives to deviate from the recommendation; thus, user compliance can be ensured. Several recent studies in equilibrium routing also share similar insights while incorporating machine learning techniques to improve traffic prediction or users’ route choice behaviors.

Papers

• L. Du, L. Han, and X.-Y. Li, “Distributed coordinated in-vehicle online routing using mixed-strategy congestion game,” Transportation Research Part B: Methodological, vol. 67, pp. 1–17, 2014.
• L. Du, S. Chen, and L. Han, “Coordinated online in-vehicle navigation guidance based on routing game theory,” Transportation Research Record, vol. 2497, no. 1, pp. 106–116, 2015.
• N. Mahajan, A. Hegyi, S. P. Hoogendoorn, and B. van Arem, “Design analysis of a decentralized equilibrium-routing strategy for intelligent vehicles,” Transportation Research Part C: Emerging Technologies, vol. 103, pp. 308–327, 2019.
• B. Zhou, Q. Song, Z. Zhao, and T. Liu, “A reinforcement learning scheme for the equilibrium of the in-vehicle route choice problem based on congestion game,” Applied Mathematics and Computation, vol. 371, p. 124895, 2020.

Between system efficiency and user equilibrium

Therefore, many research efforts aim to bridge the gap between system efficiency and user equilibrium. They strive to minimize overall system costs associated with individually optimizing or user equilibrium recommendations to a certain desired level.

Within this domain, two main research trends have emerged: one focuses on minimizing overall system costs while accounting for user preferences or selfish choice behavior constraints, and the other strategically designs or perturbs the information received by users to align user preferences with system efficiency.

Papers

• M. van Essen, T. Thomas, E. van Berkum, and C. Chorus, “From user equilibrium to system optimum: a literature review on the role of travel information, bounded rationality and non-selfish behaviour at the network and individual levels,” Transport Reviews, vol. 36, no. 4, pp. 527–548, 2016.
• V. Morandi, “Bridging the user equilibrium and the system optimum in static traffic assignment: a review,” 4OR, pp. 1–31, 2023.
• Y. Ning and L. Du, “Robust and resilient equilibrium routing mechanism for traffic congestion mitigation built upon correlated equilibrium and distributed optimization,” Transportation research part B: methodological, vol. 168, pp. 170–205, 2023.
• S. Spana, L. Du, and Y. Yin, “Strategic information perturbation for an online in-vehicle coordinated routing mechanism for connected vehicles under mixed-strategy congestion game,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 5, pp. 4541–4555, 2021.