Resource Allocation for Decomposable DNN in Edge–IoT Framework

Link to Paper (This work is published in IEEE Internet of Things Journal): https://ieeexplore.ieee.org/abstract/document/9953097

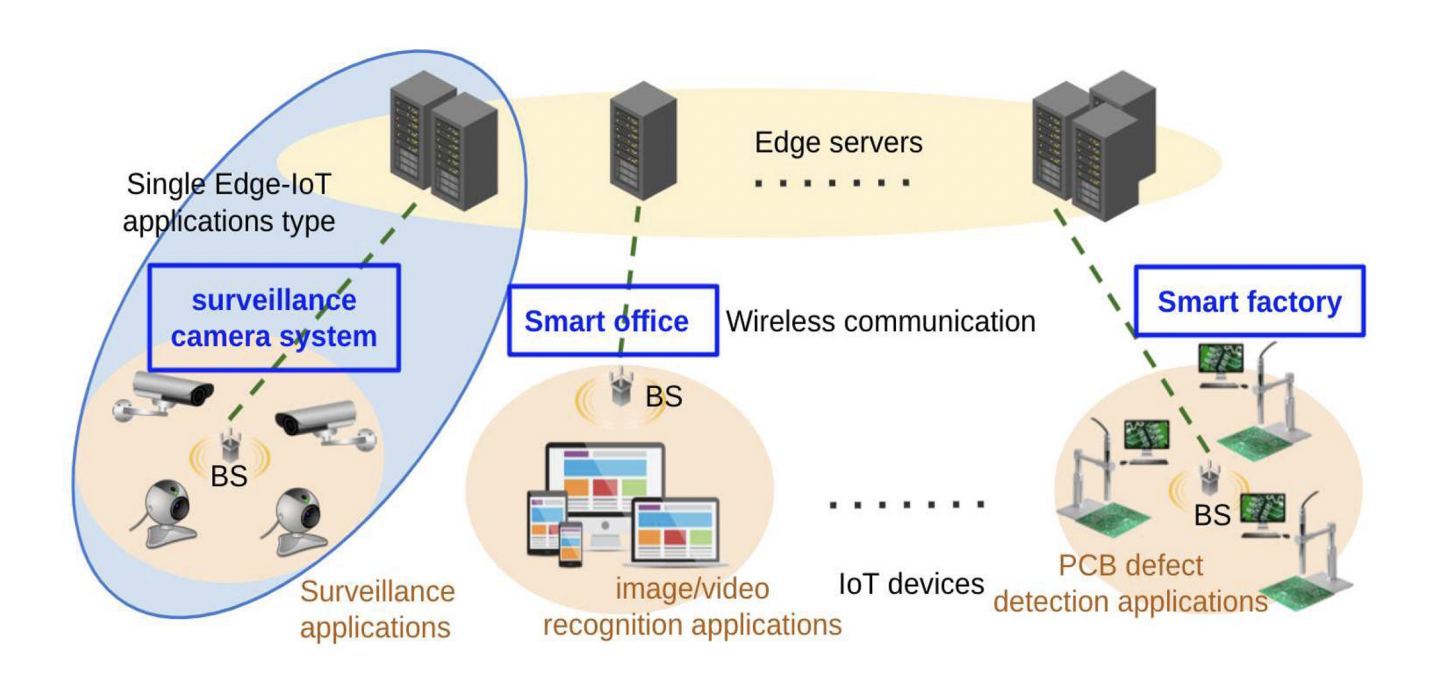
Motivation

Deep learning (DL) applications have attracted significant attention with the rapidly growing demand for Internet of Things (IoT) systems. However, performing the inference tasks for DL applications on IoT devices is challenging due to the large computational demands of DL models. Recently, edge computing has offered us a solution by deploying resources near the end users. However, resources at the edge are still limited; thus, management issues, such as allocating the networking resources as well as the computing capabilities and configuring the devices appropriately for different applications, become essential.

Our approach

For knobs in edge management, we consider multiple application tasks with different options of DL models and different hyperparameter settings, along with possible decomposition points that utilize the split DL concept to design the configuration tables. Layer-level decomposition in split DL provides greater flexibility by splitting a single DL inference model into parts on different computing devices, and each part consists of several consecutive layers. We then propose the SplitDL-Image and the SplitDL-Video algorithms based on the Vickrey–Clarke–Groves (VCG) mechanism by considering model performance and frames per second (FPS) requirements with the preferences of the heterogeneous IoT devices. The proposed method allocates networking and edge server computing resources according to the designed configuration tables by assigning the appropriate configuration to each IoT device.

Brief Introduction to VCG

A VCG mechanism consists of $n$ strategic players and a finite set $\Omega$ of possible auction outcomes. Each player $i$ has a private valuation $v_i(\omega)$ for each outcome $\omega \in \Omega$. If assumed truthful bids, the allocation rule is to select an outcome $\omega^*=X(bid)$ that maximizes the sum of bids.

Then, the payment function is designed as

where $\omega^*=X(bid)$, in order to charge bidder (player) $i$ for its externality. This would make bidders tend to bid the true valuations as their dominant strategy. As a result, the utility \(u_i(\omega)\) for each bidder $i$ in outcome $\omega$ will be their private value minus their VCG payment as

Properties for VCG

Recall that the VCG mechanism is to (1) assume truthful bidding, pick the welfare-maximizing outcome due to the demand for welfare maximization, and (2) define a payment rule that leads to a DSIC mechanism. Besides, it also guaranteed us individual rationality (utilities of players are not negative) and weakly budget balance (total payment to central(auctioneer) is not negative).

Social Surplus Maximization

We can get social surplus maximized since we define our allocation rule as directly pick the welfare-maximizing outcome.

Truthful bidding (DSIC)

If we fix bidder $i$ and the bids of other bidders $bid_{-i}$, when the outcome $X(bid)$ chosen by the allocation rule is $\omega^*$, bidder $i$’s utility would be

Note that the term in the second bracket is independent of what bidder $i$ bids, so the utility-maximizing problem reduces to maximizing the terms in the first bracket. If bidder $i$ bids $bid_i = v_i$, then the terms in the first bracket will be identical to what the mechanism wants to maximize in eq.(1). Hence, we know that bidding truthfully would result in the VCG mechanism choosing an outcome that not only maximizes welfare but also maximizes bidder $i$’s utility.

Individual Rationality

Individual rationality is also a property that the VCG mechanism guaranteed. Followed by the terms above and if bidder $i$ bids $bid_i = v_i$ ,

Then, since $\omega^*$ is the outcome that maximizes social welfare,

And from no negative externalities, which means that the utility of any choice that each player can make without the player’s participation is zero or positive, $bid_i(\omega) \geq 0$, we can get

thus $u_i(\omega^*)$ is non-negative.

Weakly Budget Balance

VCG mechanism also provides weakly budget balance property when the no single-agent effect holds. If bidder $i$ bids $bid_i = v_i$,

By no single-agent effect property, that is, the sum of welfares of agents without $i$ is weakly increased by dropping $i$ from the auction,

We prove that the sum of transfers (payments) from bidders to the center is non-negative.

Concerns

• Complexity

Results

Simulation results based on real-world applications show that the proposed method indeed allocates more resources to IoT devices with more urgent/important tasks, preference for better accuracy, or higher local computational cost. In addition, other desired properties in auctions, such as truthful bidding, individual rationality, and weakly budget balance, are also guaranteed.

Some related research papers

Model-level task decomposition

• Inference the models in the task pipeline on different computing devices
  

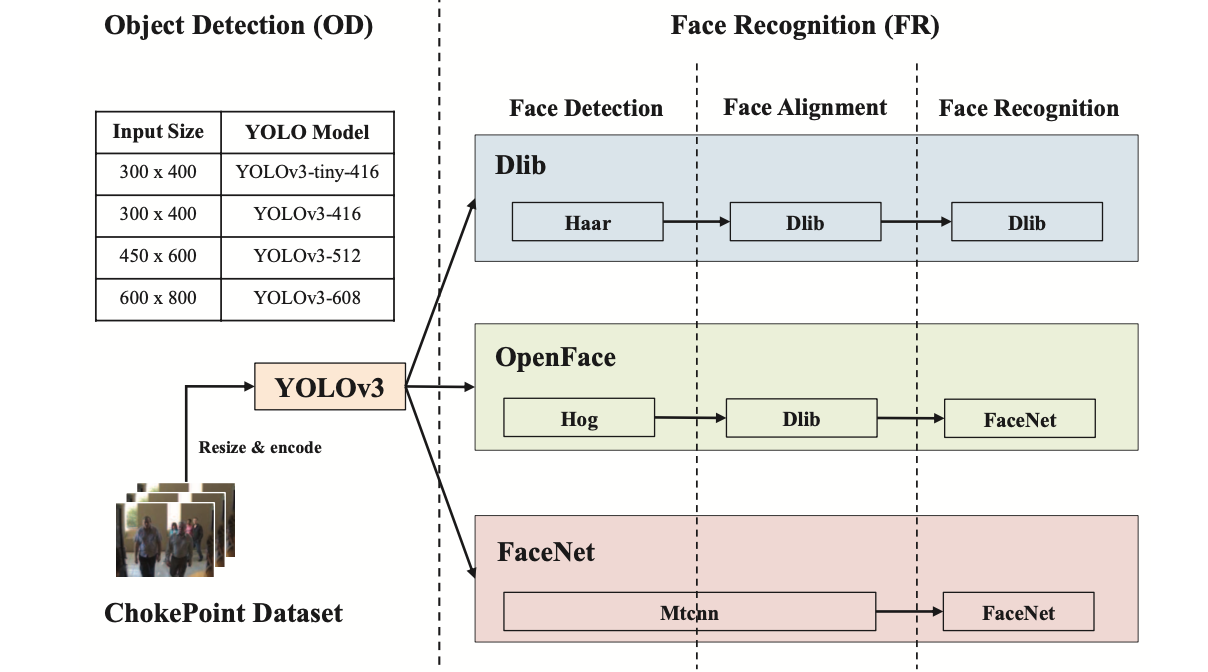From: Y. Zhang, J.-H. Liu, C.-Y. Wang, and H.-Y. Wei, “Decomposable intelligence on cloud-edge iot framework for live video analytics,”IEEE Internet of Things Journal, vol. 7, no. 9, pp. 8860–8873, 2020.

Papers:

• C.-C. Hung, G. Ananthanarayanan, P. Bodik, L. Golubchik, M. Yu,P. Bahl, and M. Philipose, “Videoedge: Processing camera streams using hierarchical clusters,” in 2018 IEEE/ACM Symposium on Edge Computing (SEC), 2018, pp. 115–131.
• Y. Zhang, J.-H. Liu, C.-Y. Wang, and H.-Y. Wei, “Decomposable intelligence on cloud-edge iot framework for live video analytics,”IEEE Internet of Things Journal, vol. 7, no. 9, pp. 8860–8873, 2020.

Layer-level decomposition

• Run the inference of different layers in a single DL model on different computing devices
• Motivated by the difference of output data size between each DL layer → lead to different requirements of the networking resource
  

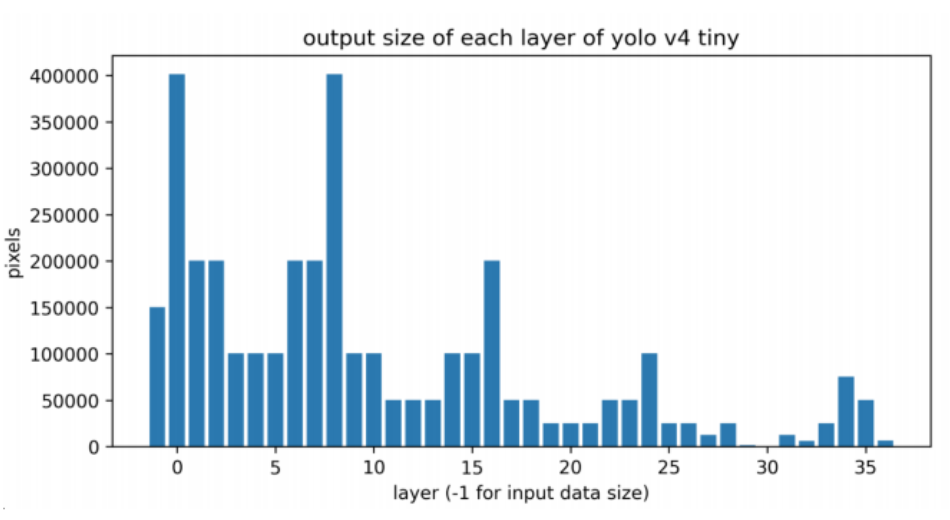
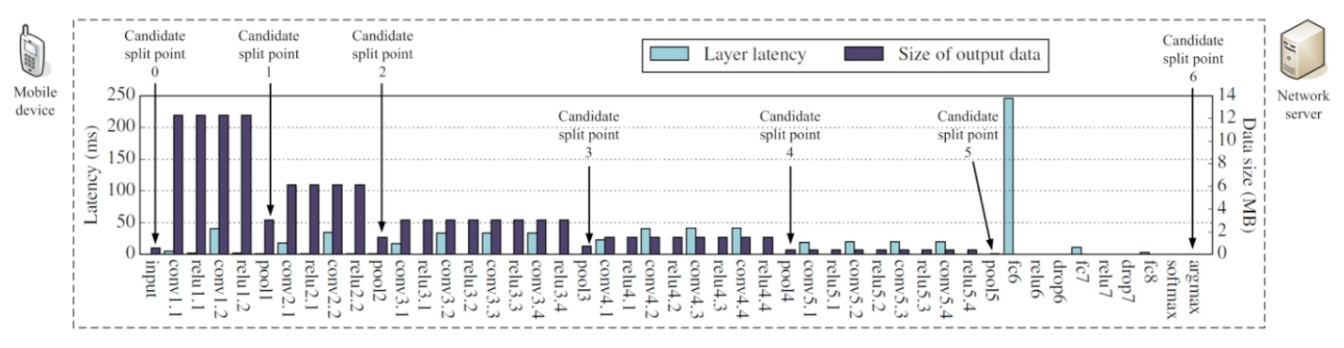
• In the case of a single model with fixed variables, if the network situation and the capabilities of devices are known, we can find the best point for layer-level decomposition. Ex:

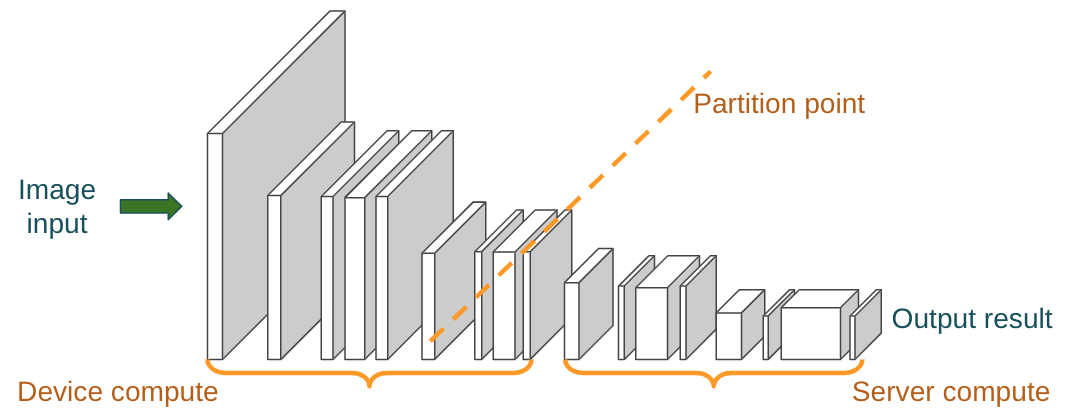
• When the network situation is unknown, there may be multiple possible locations where partitions can be made, and if there are multiple kinds of tasks, multiple choices of models with different parameter settings that lead to different accuracy, it will be much more complicated

From: 3GPP, “5G System (5GS); Study on traffic characteristics and performance requirements for AI/ML model transfer,” 3rd Generation Partnership Project (3GPP), Technical Report (TR) 22.874

Papers

• J. Zhou, Y. Wang, K. Ota, and M. Dong, “Aaiot: Accelerating artificial intelligence in iot systems,”IEEE Wireless Communications Letters,vol. 8, no. 3, pp. 825–828, 2019.
• E. Li, L. Zeng, Z. Zhou, and X. Chen, “Edge ai: On-demand accelerating deep neural network inference via edge computing,”IEEE Transactionson Wireless Communications, vol. 19, pp. 447–457, 2020.
• L. Zeng, E. Li, Z. Zhou, and X. Chen, “Boomerang: On-demand cooperative deep neural network inference for edge intelligence on the industrial internet of things,”IEEE Network, vol. 33, no. 5, pp. 96–103,2019.
• C. Hu, W. Bao, D. Wang, and F. Liu, “Dynamic adaptive dnn surgery for inference acceleration on the edge,” in IEEE INFOCOM 2019 - IEEE Conference on Computer Communications, 2019, pp. 1423–1431.

Parallel decomposition

• parallel decomposition divides the input data frame into several patches and performs the inference computation in parallel on different devices.

Papers

• Z. Zhao, K. M. Barijough, and A. Gerstlauer, “Deepthings: Distributed adaptive deep learning inference on resource-constrained iot edge clusters,”IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 37, no. 11, pp. 2348–2359, 2018.
• R. Hadidi, J. Cao, M. S. Ryoo, and H. Kim, “Toward collaborative inferencing of deep neural networks on internet-of-things devices,”IEEE Internet of Things Journal, vol. 7, no. 6, pp. 4950–4960, 2020.
• L. Zeng, X. Chen, Z. Zhou, L. Yang, and J. Zhang, “Coedge: Cooperative dnn inference with adaptive workload partitioning over heterogeneous edge devices,”IEEE/ACM Trans. Netw., vol. 29, no. 2, p. 595–608, apr2021. [Online]. Available: https://doi.org/10.1109/TNET.2020.3042320

Both parallel and layer-level

Papers

• T. Mohammed, C. Joe-Wong, R. Babbar, and M. D. Francesco, “Distributed inference acceleration with adaptive dnn partitioning and offloading,” in IEEE INFOCOM 2020 - IEEE Conference on ComputerCommunications, 2020, pp. 854–863.
• E. Kilcioglu, H. Mirghasemi, I. Stupia, and L. Vandendorpe, “An energy-efficient fine-grained deep neural network partitioning scheme for wireless collaborative fog computing,”IEEE Access, vol. 9, pp.79611–79627, 2021.